Pre-print “Shot-noise reduction for lattice Hamiltonians”
In our recent work, by Timo Eckstein, Refik Mansuroglu, Stefan Wolf, Ludwig Nützel, Stephan Tasler, Martin Kliesch, and Michael J. Hartmann, that has just been published as a preprint: https://arxiv.org/abs/2410.21251, we present an energy estimation technique that is tailored to quantum lattices systems to obtain particularly efficient readout circuits yielding a guaranteed sampling noise reduction.
In quantum computing, in contrast to its classical counterpart, the result of our computation is typically not a single deterministic bitstring but a hard-to-classically obtain probability distribution encoded into a quantum state. Hence, a central task after state preparation is to efficiently extract information from this probability distribution, i.e. efficiently measuring the generated quantum state. Particularly relevant near-term measurement tasks are those for energy estimation of quantum material low-energy stats as they are considered an enabler for material science research via quantum computing.
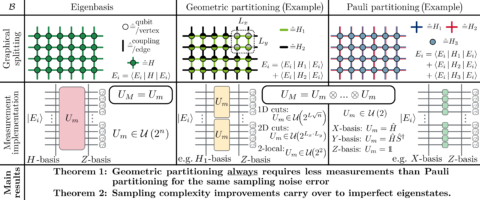
Here, we present geometric partitioning as a measurement scheme for estimating the energy of quantum lattice models. It splits the Hamiltonian into subsystems that extend over multiple lattice sites, for which transformations between their local eigenbasis and the computational basis can be efficiently found. This allows us to reduce the number of measurements as we sample from a more concentrated distribution without diagonalizing the problem. For systems in an energy eigenstate, we prove a lower bound on the sampling number improvement over the “naive” mutually commuting local operator grouping, which grows with the considered subsystem size, consistently showing an advantage for our geometric partitioning strategy. Notably, our lower bounds do not decrease but increase for more correlated states (Theorem 1). For states that are weakly isotropically perturbed around an eigenstate, we show how the sampling number improvement translates to imperfect eigenstate improvements, namely measuring close to the true eigenbasis already for smaller perturbations (Theorem 2).
We expect our results to have a noticeable positive impact on NISQ eigenstate preparation algorithms as those typically need to estimate the state’s energy numerous times. Importantly, the patch size can be freely chosen to fit the available gate budget, starting from as little as n/2 additional 2-qubit gates, which are simply appended to the end of the existing quantum circuit.
We acknowledge support from FAU Erlangen-Nürnberg, Max Planck Institute for the Science of Light, Universität Wien | University of Vienna, Hamburg University of Technology, Erlangen National High Performance Computing Center (NHR@FAU), Deutsche Forschungsgemeinschaft (DFG) – German Research Foundation (QuCoLiMa), FAU Profile Center Light.Matter.Quantum Technologies, Bundesministerium für Bildung und Forschung (EQUAHUMO), IMPRS Physics of Light, Fujitsu Germany GmbH and Bavarian State Ministry of Science and the Arts via Munich Quantum Valley, Elite Network of Bavaria, Hightech Agenda Bavaria